Variance
Gy defines the fundamental variance for a sample S to be the relative variance of the sample’s critical content, aS, when the sample is correct and fragments are selected for S independently of each other (i.e., in independent Bernoulli trials). He estimates the fundamental variance using the following equation.
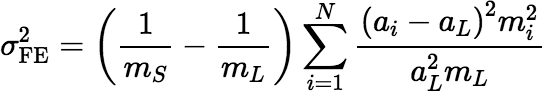
The fundamental variance is considered to be the smallest relative sampling variance that is practically achievable without increasing the sample size or reducing the fragment sizes (i.e., grinding or milling the material before sampling). In routine practice, one can expect the sampling variance to be somewhat larger than the fundamental variance, but any additional variance tends to be harder to estimate.
Equation 1 can be derived by a technique sometimes called uncertainty propagation
or
error propagation.
Using error propagation, one estimates the relative variance
of aS by:
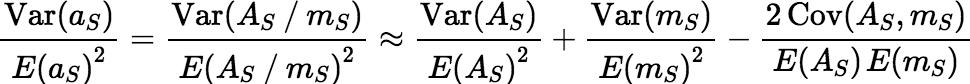
When one makes Gy’s assumptions, with the selection probability for each fragment equal to p = mS / mL, and substitutes exact expressions for Var(AS), E(AS), Var(mS), E(mS), and Cov(AS, mS) into Equation 2, one obtains Equation 1 for the fundamental variance.
One may also derive an expression for the sampling variance under the assumption that S is a random sample of exactly k fragments from the lot (for some positive number k). The fact that S is a random sample of size k means that for all subsets G of L of size k,
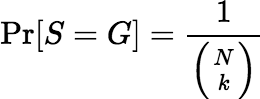
Under this assumption, Equation 2 yields a slightly different expression for the relative variance, which is shown below.
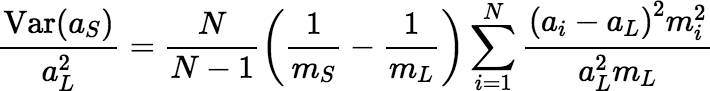
Equation 4, which was derived for a correct sample, S, seems also to work well enough for a fair sample, SF, of size k such that for all subsets G of L of size k,
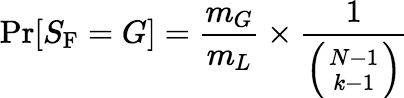
And of course, SF has the advantage of being provably unbiased, so that E(aSF) = aL.
Both Equation 1 and Equation 4 are only approximately true, but they can be applied to many real-life situations in the laboratory. There is another equation that is exactly true, but which obviously does not apply to many real-life situations in the lab.
Theorem Suppose m1 = m2 = ⋯ = mN and S is a sample such that Pr[S = G] = Pr[S = H] whenever |G| = |H|. Then:
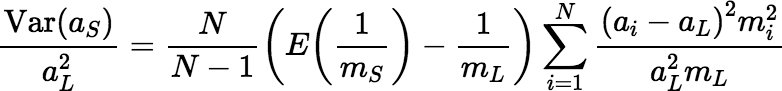
When all the fragment masses are equal, selecting fragments for the sample in independent Bernoulli trials makes the premise of the theorem true.* So, in this case at least, Gy’s equation for the fundamental variance is a good approximation, except for the missing factor N / (N − 1), which is near unity when N is large, and therefore can be neglected.
Generally, one may expect Equation 1 to be a good approximation as long as the relative standard deviation of mS is small. If RSD(mS) is large, say because the sample is too small or there are some very massive fragments in the lot, the approximation may be much worse.
It is proved elsewhere that when the sampling is correct, keeping RSD(mS) small also ensures that the sampling bias is negligible in comparison to the standard deviation.
* Well, there is the minor issue of the empty sample. If one selects all the
fragments in independent Bernoulli trials, it is possible that no fragments will be selected at all.
In that case the sampling must be repeated until a nonempty set of fragments is obtained, but the premise of the
theorem is still true. It is possible to avoid the problem by selecting the first fragment correctly
and then selecting all the other fragments in independent Bernoulli trials using Gy’s procedure. The sampling
is still correct
and there is no danger of an empty sample. Or, to ensure the sample is truly unbiased,
select the first fragment with each fragment’s selection probability proportional to its mass. This approach
theoretically produces a nonempty and unbiased sample, but it is even more impractical than the original.