Mathematics

More ideas (maybe):

• The mathematics of rotation in ℝⁿ and representing the orientation of a k-dimensional polytope in ℝⁿ (related to the Hyper screen saver)
  
  
• The most interesting mathematical subject I’ve encountered since graduation: geometric algebra
• The noncentral t-distribution and the noncentral χ²-distribution
• Introduction to the most basic concepts of topology and measure theory (leading to continuous functions and measurable functions)
• Some math related to the problem of unbiased sampling of particulate material (and laboratory subsampling) — For a lot consisting of n particles, the sampling schemes that are guaranteed to be unbiased can be represented as a convex polytope in a high-dimensional real vector space (but how many vertices does this polytope have?)

Problem 1: Tom, Dick, and Harry competed in a track-and-field meet where points were awarded for first, second, and third place in each event. At the end of the meet, Tom had 22 points, Dick and Harry had 9 points each, and nobody else had any points.

If Dick won the javelin throw, who finished second in the 100-yard dash?

Problem 2: The following algorithm calculates the first several terms (0 through n) of a well-known integer sequence. Can you determine which one?

A Note About Notation: Power Sets

My years of math education led me to believe, mistakenly it seems, that the common symbol for a power set was a script capital P with a particular form: . For example, below are photos taken from three different textbooks, by three different authors, from three different publishers.^1, 2, 3

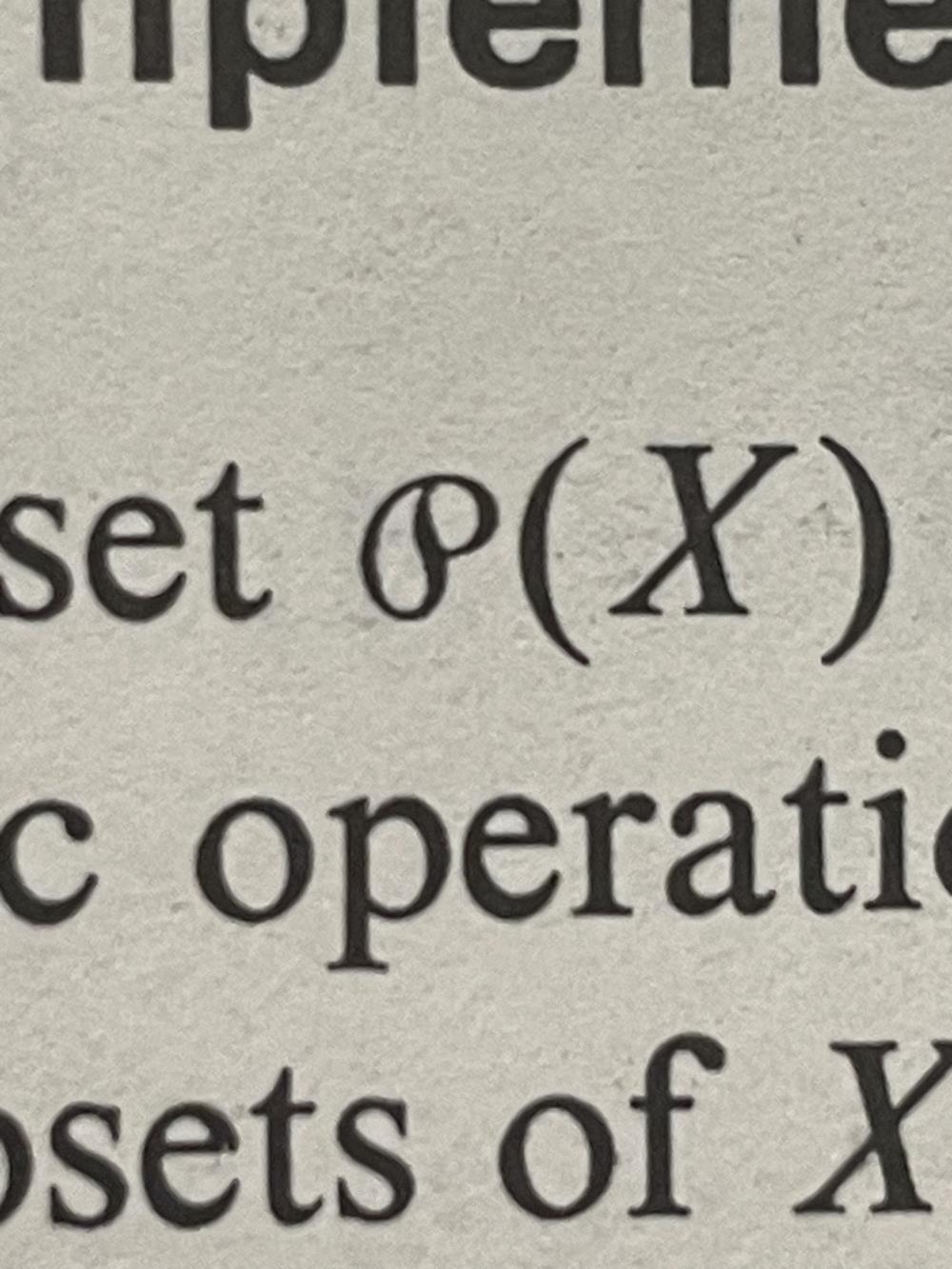
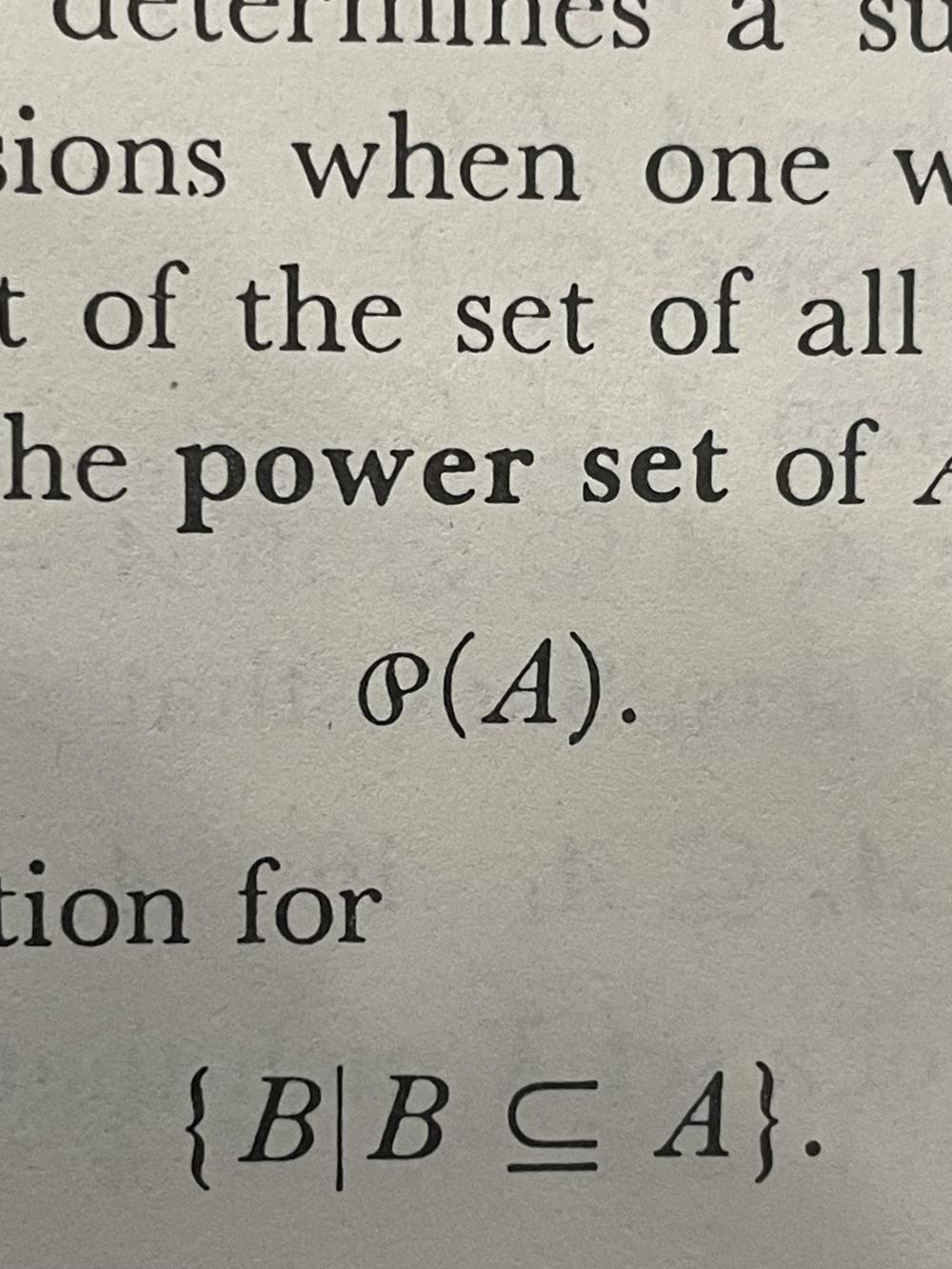
Other books used various notations, including P(X), 𝒫(X), and [X], but (X) appeared to be most favored—the symbol any author would want to use if it were available.

It is surprisingly difficult to find this glyph online. It was never part of standard TeX, and it doesn’t have a special Unicode symbol. Initially, W3C appeared to recommend using the Weierstrass ℘, but Unicode recommended the mathematical script capital 𝒫, which is probably a better choice. Although the curves of ℘ resemble those of , the symbol ℘ has another meaning. The only problem with 𝒫 from my point of view is that one might want to use it for other purposes, along with other script capital letters, like 𝒜, ℬ, 𝒞, …. The concept of a power set is important enough to deserve its own unique symbol.

When I had trouble finding the glyph I wanted online, I photographed an example from a textbook (Munkres), trimmed it down, used it in a Google image search, and still came up empty. Eventually, I did a little more processing of the image and made my own PNG version, which is a little crude at full scale (below) but not bad when reduced (). Copy it if you like, or send me a better version if you have one (SVG?).

It’s possible that this symbol is just a variant of ℘, but it looks like an uppercase letter, unlike the lowercase ℘. I believe that the second edition of Munkres used a more ordinary script capital P; so, perhaps my symbol, whatever it is, was popular for only a short period of time.