Geometry Factors
Since the intrinsic detection efficiency of the alpha-particle detector in a typical alpha-spectrometry chamber is nearly 100 %, the overall efficiency of the counting system for a thin alpha-emitting source is essentially the same as the geometry factor, defined as the mean solid angle subtended by the detector window at the source, divided by 4π. So, if you know the dimensions of the detector and the source, and their relative positions and orientations, in principle you can predict the efficiency without a calibration. Or, if you measure the efficiency for a source in one geometry, you can apply a correction factor to estimate the efficiency for a different geometry.
In the equations below we’ll use spherical coordinates (ρ, θ, ϕ), cylindrical coordinates (r, θ, z), and Cartesian coordinates (x, y, z), which are related to each other as follows:
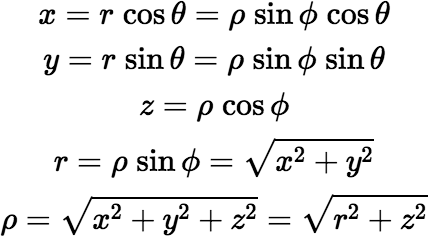
Visualize the xy-plane (ϕ = π / 2) as horizontal, with the positive z-axis, or polar axis (ϕ = 0), rising upward.
Solid Angle Subtended by a Disk at a Point on its Axis
The solid angle Ω subtended by a surface D at a point not on the surface is generally given as an integral, which may be a surface integral or a line integral (around the boundary). In spherical coordinates the solid angle subtended by D at the origin is given by the surface integral:
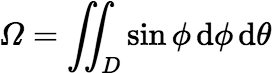
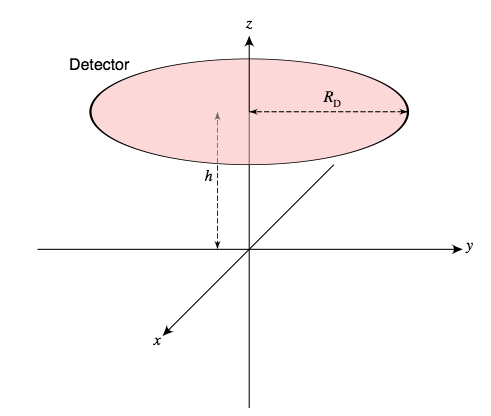
The active window of an alpha-spec detector is typically a flat disk. Let RD denote the radius of the disk and assume the disk is centered on the polar axis, parallel to the xy-plane at a fixed height h above it, as shown below
In this case the surface integral yields the following equation for the solid angle subtended by the disk at the origin:
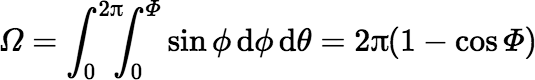
where Φ is the polar angle ϕ at the rim of the disk. The cosine of this angle is given by
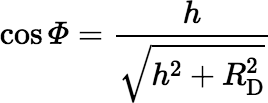
So, we get:
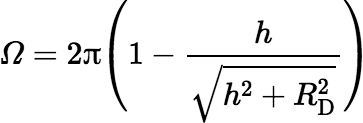
Although this expression is theoretically exact, in actual calculations it can produce large round-off errors if h ≫ RD. In these situations it is better to apply a few trig identities and compute Ω using an equation that is less susceptible to the effects of rounding. For example,
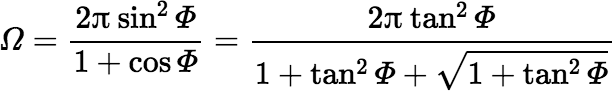
where tan Φ = RD / h and we use the fact that 0 ≤ Φ < π/2. The following version should suffice as long as either h > 0 or h = 0 and RD > 0 (and neither h nor RD is huge).
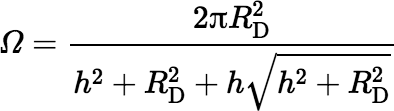
Solid Angle Subtended by an Ellipse
Suppose now that D has an elliptical shape wtih semi-major axis a, semi-minor axis b, eccentricity e, and maximum polar angle Φ, but it is still centered on the polar axis at a height h above the horizontal plane. (Note that tan Φ = a / h.) Now the solid angle subtended by D at the origin can be shown to be
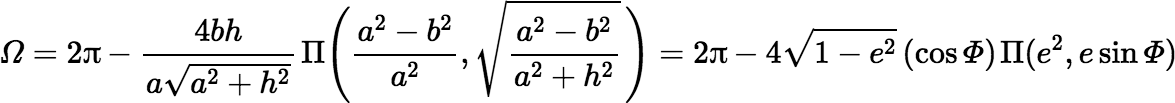
where Π(n, k) denotes a complete Legendre elliptic integral of the third kind, which is defined by the following equation.
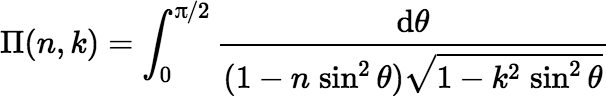
Note: There are several variants of the definition of the function Π. I favor the one used by Wolfram, which uses k instead of sin α but which in other respects is compatible with the one used by Abramowitz and Stegun. The definition that appears in Numerical Recipes (see below), uses a different sign convention for n.
If you can calculate this elliptic integral accurately, you can calculate Ω accurately, at least when the value of Ω is not too small. If it is too small, the fact that it is obtained as the difference between 2π and another number that is almost equal to 2π implies that round-off error can be relatively large.
The value of Ω will be small if either Φ ≈ 0 (a / h ≈ 0) or e ≈ 1 (b / a ≈ 0). When Φ ≈ 0, the solid angle is approximated well by the quotient of the area of D and h2. Note: I’m sure there are better approximations.
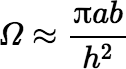
Suppose instead that e ≈ 1. As e → 1 from below, the value of the elliptic integral increases without bound. A useful approximation in this case is:
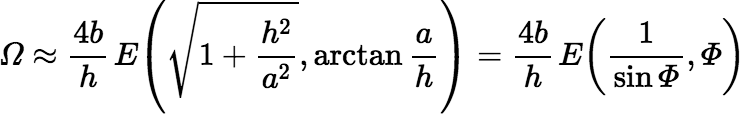
where E(k, ϕ) denotes an elliptic integral of the second kind. If Φ is too small, the preceding approximation should be easier to calculate.
Solid Angle Subtended by a Disk at a Point Not on Its Axis
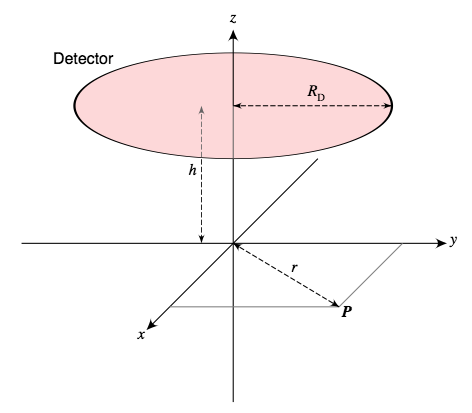
Next suppose D is again a disk but now consider the solid angle subtended by D at a point P in the xy-plane at a distance r from the origin.
The solid angle subtended by the disk D at P is the same as the solid angle subtended by the image of the disk obtained by a 3-D perspective transformation, where the view plane is oriented so that the image is an ellipse centered on the orthogonal line that passes through the center of projection P. The trick then is to find the parameters of that ellipse The following equations provide the necessary values; however, rounding error can be an issue in some circumstances.
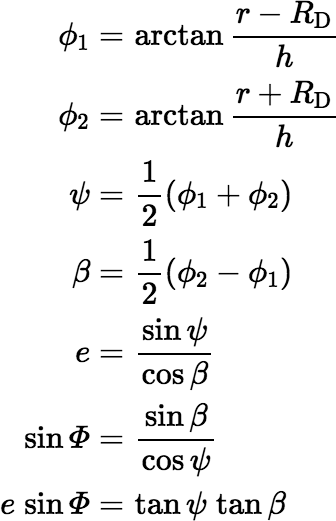
If we define
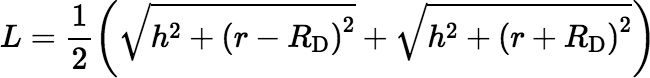
then we get a substantial simplification, as shown below.
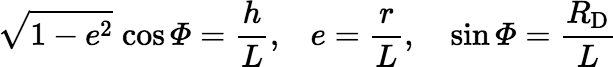
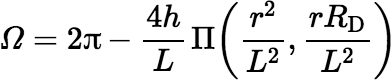
When you use this equation for Ω, there is little reason to worry about round-off error until you calculate the elliptic integral and perform the final subtraction from 2π.
I use Carlson’s method for evaluating the elliptic integral, as presented in Numerical Recipes [Press et al., 1992, 2007]. For extreme values of the arguments that make Ω very small, you can expect large relative errors due to rounding in the final subtraction. The rounding error can be reduced in some cases by the use of a series for the elliptic integral. For example,
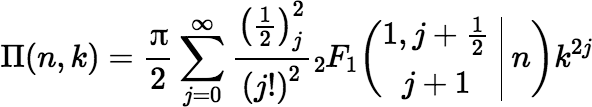
where n = e2 = r2 / L2 and k = r RD / L2 and where 2F1 denotes the Gauss hypergeometric function:
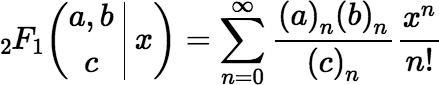
In the equation above for Ω, the value of Π(n, k), multiplied by 4h / L, is subtracted from 2π. The first term of the series, where j = 0, can be subtracted from 2π with good accuracy, leaving the higher-order terms to be subtracted. If e is not large (because P is not too far from the axis), those remaining terms are relatively small and do not cause large rounding errors. (If e = 0, all the higher-order terms are zero, because n = k = 0.)
The Geometry Factor for an Extended Source
Using this approach you obtain a function Ω(r) for the solid angle defined in terms of the distance r of P from the origin, assuming fixed values for RD and h. The geometry factor for an extended source is defined to be the mean solid angle averaged over all points of the source, which is calculated by another integral.
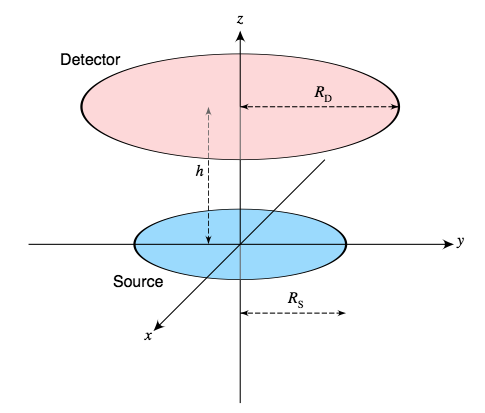
Given the function Ω(r), the required integral for a disk-shaped source of nonzero radius RS (see above) can be calculated using a good technique for numerical integration, such as Gaussian quadrature or Simpson’s Rule.
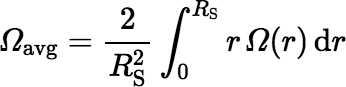
If h is not too small, Gaussian quadrature is likely to give excellent results; but be careful with this technique when h is very small and RS > RD or RS ≈ RD, because the solid angle Ω(r) is almost a step function in the vicinity of r = RD, dropping steeply from Ω ≈ 2π to Ω ≈ 0 as r increases. In this case you can use Simpson’s Rule, which is robust and amenable to brute-force processing; or if h is small enough, you can use the fact that:
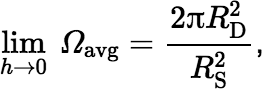 for RS > RD
for RS > RDFor RS < RD, the limit is just 2π.
To be completed: (1) There are other equivalent equations for Ω(r) that can be derived directly from the surface integral; however, my versions of these, shown below, are less simple than those shown above.
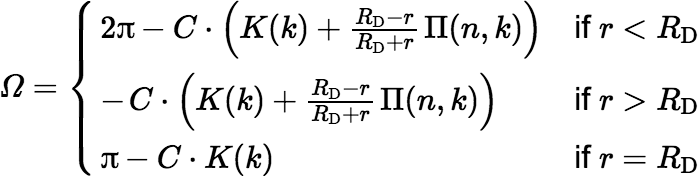
where K(k) denotes the complete elliptic integral of the first kind and where
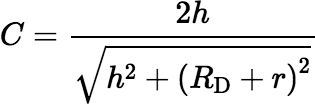 ,
, 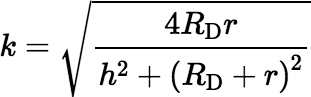 , and
, and 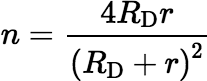
For r ≈ RD but r ≠ RD, these alternative equations are probably not great for actual calculations. And when the solid angle is small, you still need to do some work to avoid large rounding errors. (2) It is easier to calculate the solid angle subtended by a polygon than the solid angle subtended by a disk. Approximating the disk by a regular polygon with the same area is a good practical option in the lab. (3) Monte Carlo simulation is another popular approach, although it is inherently inexact. On the other hand it can provide explicit uncertainty estimates. (4) After my coworker described his use of my calculations at a radiochemistry conference in October 2014, I knew I needed to complete my work on evaluating the combined standard uncertainty of the geometry factor. I have done that now but I need to write it up clearly. (5) James Clerk Maxwell discussed the solid angle subtended by an ellipse in A Treatise on Electricity and Magnetism, Chapter XIV. He mentioned a solution using the elliptic integral of the third kind but preferred a different solution in terms of an infinite series of spherical harmonics.
Updates: In 2017 I discovered the work of John T. Conway, who published a nice paper on this subject in 2006. He provided a closed-form expression for the average geometry factor in terms of elliptic integrals and also an integral that seems to give highly accurate results without much work. I have not explored all the cited references, but I recommend the paper anyway: “Generalizations of Ruby’s formula for the geometric efficiency of a parallel-disk source and detector system,” Nuclear Instruments & Methods in Physics Research. A 562 (2006) 146–153.