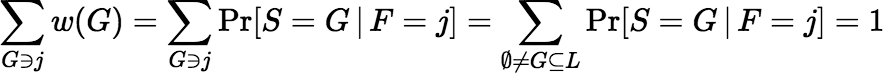Bias – p. 3
Subsampling Bias (Continued)
This page takes you down the rabbit hole.
Since there is a difference between stating that a sample is unbiased and stating that it is unbiased for all possible values of a1, a2, …, aN, we offer the following definition.
When the sample consists of only one fragment, it is easy to eliminate
sampling bias: simply make each fragment’s selection probability
proportional to its mass, as in the example described earlier. It is not
completely obvious how to generalize this sampling strategy when the sample
consists of more than one fragment. However, while studying Gy’s
sampling theory and considering his definition of
correct
sampling, I (Keith) proved the result shown below as
Theorem B.1. If you were already aware of this theorem,
please email me at Work@mccroan.com.
The theorem describes sufficient conditions to ensure that the
sampling bias for a single sample is zero. (The conditions are sufficient but not necessary.)
Theorem B.1 Let F be a random member of L, and let R be a random subset of L \ {F} such that:
- the index F and the size |R| are independent random variables,
- Pr[ F = j ] = mj / mL for all j ∈ L, and
- for all integers j ∈ L and all subsets G and H of L \ { j }, if |G| = |H|, then Pr[ R = G | F = j ] = Pr[ R = H | F = j ].
Let S = {F} ∪ R,
where ∪
denotes union of sets. Then S is fair.
The theorem implies that to ensure the sample is unbiased, it suffices to choose
the first fragment for the sample on the basis of mass (i.e., with each fragment’s selection probability
proportional to its mass) and then to select all the other fragments at random,
with the added condition that the number of fragments
selected cannot be dependent on which fragment is chosen first.
So, although completely correct
sampling as defined by Gy does not guarantee zero bias, there are bias-free methods of sampling that are
incorrect
only in the manner of selecting the first fragment.
The theorem is presented above in the form I first imagined, thinking of an actual procedure for choosing the fragments of the sample. A mathematically simpler form appears below as Corollary B2.2. The version that appears below makes it explicit that the conditional probability Pr[ R = G | F = j ] in part (iii) above is a function of the number of fragments |G| and does not depend on j.
Example:
Suppose a lot contains 4 fragments, with masses 1, 2, 5, and 12 (grams). How can
one take a sample consisting of exactly two fragments in a manner that
guarantees the expected critical content of the sample equals the critical content of the lot?
Answer: Choose the first fragment on the basis of mass. Then choose one of the remaining
fragments at random, without regard to mass. When the first fragment is selected, the
selection probabilities are as follows:
| Fragment | Mass / g | Selection probability |
| A | 1 | 1/20 |
| B | 2 | 1/10 |
| C | 5 | 1/4 |
| D | 12 | 3/5 |
E.g., suppose fragment D is chosen first (as it will be three times out of five). Then each of the other three fragments (A, B, C) has probability 1/3 of being selected as the second fragment.
Theorem B.1 implies that regardless of the actual critical content of each of the four fragments, the expected critical content of the sample equals the critical content of the lot.
The proof of Theorem B.1 uses the following lemma.
Lemma B.1.1 Let S be a sample from the lot L. Then S is fair if and only if for all j ∈ L the following equation is true:
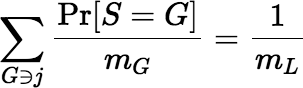
Proof:
(⇒, the only if
part)
First assume S is fair, and hence unbiased for all values of a1, …, aN.
Fix j ∈ L and for each
i ∈ L, let ai = δij, where
δ denotes the Kronecker delta. So,
Then:

So,
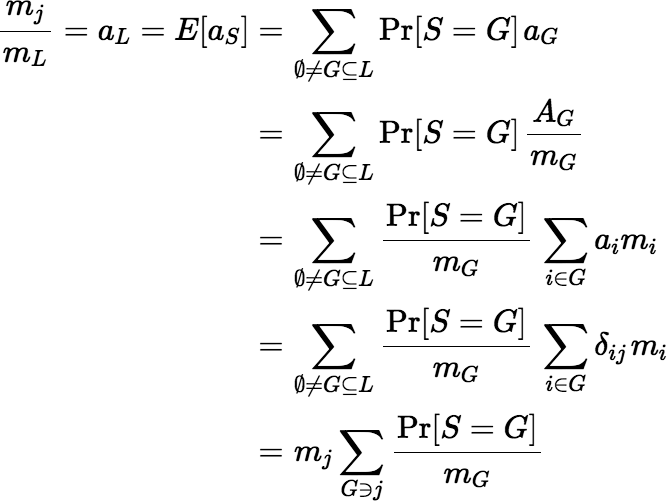
Then divide mj from both sides to get:
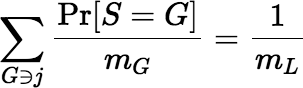
(⇐, the
ifpart) Now let a1, …, aN be arbitrary and suppose for all j ∈ L,
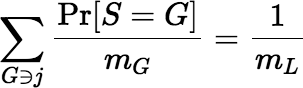
Then:
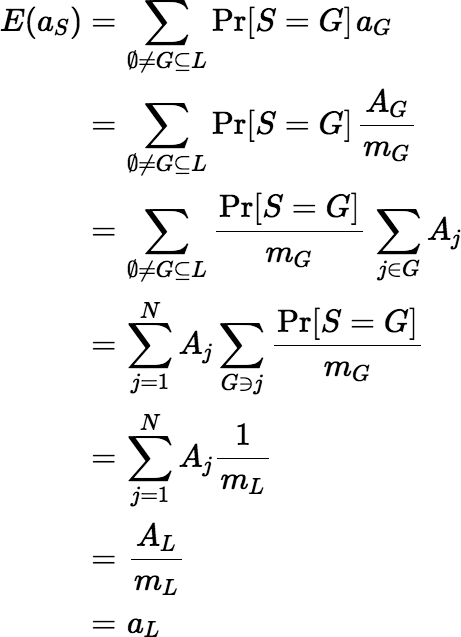
The lemma is unremarkable. If you ask yourself what it takes to ensure the sample is unbiased, you’re led quickly and naturally to this result. On the other hand Theorem B.1 wasn’t so obvious to me. I wondered for some time how to make any use of the lemma but had little insight until I came up with Theorem B.1 as a conjecture. At first it seemed ridiculous, and I thought it would be amazing if true. Then I proved that it was true, and I was amazed.
I no longer include the original proof of Theorem B.1, because I later looked for and found a more general version of the theorem, which seemed rather obvious in retrospect, but whose statement may be harder to understand at first. The more general theorem and its proof appear below.
Theorem B.2 Let F be a random member of L and S a random sample from L such that:
- Pr[ F = j ] = mj / mL for all j ∈ L, and
- there is a function w defined on the nonempty subsets of L, taking values in the interval [0,1], such that for all subsets
∅ ≠ G ⊆ L
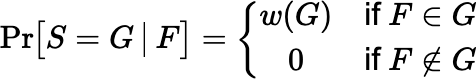
Then S is fair.
In fact any fair sample distribution can be realized in the manner of Theorem B.2—i.e., by choosing the first fragment F on the basis of mass and then completing the sample using conditional probabilities as indicated.
Now we can start to consider how to derive Theorem B.1 from Theorem B.2. First just try to rewrite Theorem B.2, like Theorem B.1, in terms of the random fragment F and the set R = S \ {F}. The result is the following corollary.
Corollary B.2.1 Let F be a random member of L and R a random proper subset of L, possibly void, such that:
- Pr[ F = j ] = mj / mL for all j ∈ L, and
- there is a function w defined on the nonempty subsets of L, taking values in the interval [0,1],
such that for all proper subsets H ⊂ L,

Let S = {F} ∪ R. Then S is fair.
The preceding corollary is still more general than Theorem B.1, but the next corollary is not.
Corollary B.2.2 Let F be a random member of L and R a random proper subset of L, possibly void, such that:
- Pr[ F = j ] = mj / mL for all j ∈ L, and
- there is a function f : {0, 1, …, N − 1} → [0,1] such that for all proper
subsets H ⊂ L,

Let S = {F} ∪ R. Then S is fair.
Corollary B.2.2 is essentially equivalent to Theorem B.1, although its presentation is mathematically simpler. To prove Corollary B.2.2 let w(G) = f (| G | − 1).
And there is the following.
Corollary B.2.3 Let F be a random member of L and R a random subset of L, possibly void, such that:
- Pr[ F = j ] = mj / mL for all j ∈ L, and
- there is a function f : {0, 1, …, N} → [0,1] such that Pr[ R = G | F ] = f (| G |) for all subsets G ⊆ L.
Let S = {F} ∪ R. Then S is fair.
This corollary differs from Corollary B.2.2 in that it allows the possibility that F ∈ R. To prove it from the main theorem, let w(G) = f (| G |) + f (| G | − 1).
Corollary B.2.4 Suppose F is a random member of L such that Pr[ F = j ] = mj / mL for all j ∈ L and Pr[ F ∈ S ] = 1. Then S is fair if and only if for all j ∈ L,
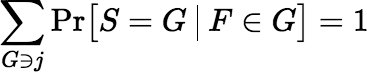
Choosing even one fragment F on the basis of mass is generally impractical because of the large number of fragments whose masses must be known. Although practicality is not really an important consideration in this analysis, a more practical approach to provably fair sampling would be to partition the N fragments into some relatively small number of nonempty cells and then choose one of those cells at random to be the sample, with each cell’s selection probability proportional to its mass. However, there are many fair sample distributions that cannot be realized in this manner. For example, if N ≥ 3, it is possible to devise a sample distribution that ensures a sample of size N − 1, but the distribution cannot be produced by partitioning the fragments into cells and choosing a cell at random, because in any partition some cells will always have sizes different from N − 1.
Lemma B.1.1 can be restated as follows:
Lemma B.1.1′ Let S be a sample from L and let Γ denote the collection of all nonempty subsets of L:
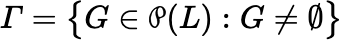
Then S is fair if and only if there is a function w : Γ → [0,1] such that:
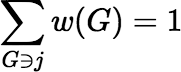 , for all
j ∈ L, and
, for all
j ∈ L, and  , for all
G ∈ Γ.
, for all
G ∈ Γ.
So, if we define the function w by
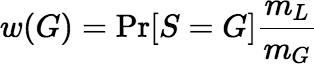 ,
then the sample is fair if and only if
,
then the sample is fair if and only if
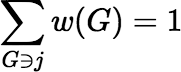 for all j. In fact, it is easy to show
that the sample is fair if and only if there is any constant c such that
for all j. In fact, it is easy to show
that the sample is fair if and only if there is any constant c such that
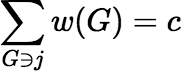 for all j, because in this case c = 1.
for all j, because in this case c = 1.
How do we interpret w(G) for a fair sample S?
If we implement S by choosing its first fragment F
with mass-based selection probabilities and then completing it as described above, then
w(G) = Pr[ S = G |
F ∈ G ].
Alternatively, if we take a random or fixed partition P of L
and then randomly select one of its cells with mass-based selection probabilities as described above, then
w(G) = Pr[ G ∈ P ].
In the latter case, the fact that
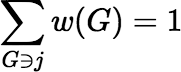 is a simple consequence of the fact that P is a partition of L.
is a simple consequence of the fact that P is a partition of L.