Bias – p. 4
Subsampling Bias (Continued)
These results are not fully developed.
We repeat the statement of Lemma B.1.1′:
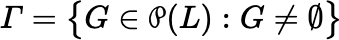
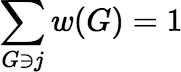 , for all
j ∈ L, and
, for all
j ∈ L, and
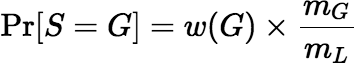 , for all
G ∈ Γ.
, for all
G ∈ Γ.
So, many properties of the collection of all fair samples can be explored by considering the somewhat more abstract collection of functions w : Γ → [0,1] such that:
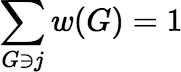 , for all
j ∈ L.
, for all
j ∈ L.
It can be shown—for what it is worth—that this collection of functions, denoted here by 𝕎N, forms a convex polytope (a bounded convex polyhedron) of dimension 2N − N − 1 in the vector space ℝΓ, which has dimension 2N − 1.
A convex polytope can be uniquely identified by its vertices. Denote the set of all vertices of 𝕎N by V(𝕎N). The size of V(𝕎N) is a rapidly growing function of N. For example, by my calculations the numbers of vertices of 𝕎N for N = 1 to 7 are as follows:
| N | Vertices |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 42 |
| 5 | 1292 |
| 6 | 200 214 |
| 7 | 132 422 036 |
The numbers in the table were determined with the assistance of a personal computer. The vertex counts for N ≥ 8 have not been calculated. It appears that the calculation for N = 8 would take years, possibly many years, using my current algorithm on a single desktop computer. (If only the value for N = 5 had been 1806 instead of 1292.)
Relating 𝕎N to Correct Samples
The polytope 𝕎N can also be related to correct
samples.
It can be shown that a sample S is correct if and only if there exists
w ∈ 𝕎N
such that Pr[S = G] =
w(G) / ‖w‖1 for
all G, where:
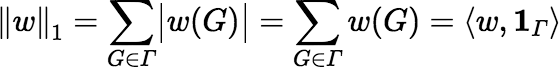
and where 1Γ is the function in ℝΓ that maps every G ∈ Γ to 1. In this case, ‖w‖1, the L1 norm of w, equals the inverse of the probability that any particular fragment will be included in S.
Significance of V(𝕎N)
There is a simple correspondence between 𝕎N
and the collection of all fair samples from L, and there is also a simple correspondence between
𝕎N and the collection of all correct samples.
So, what is the significance of V(𝕎N)?
A vertex of 𝕎N corresponds to a fair sample, S, for which the set
{G ∈ Γ : Pr[S = G] > 0}
is minimal. This set is minimal
if it has no proper subset whose
members can be assigned probabilities in a way that makes the resulting sample fair.
A vertex of 𝕎N also corresponds to a correct sample,
S, for which the set
{G ∈ Γ : Pr[S = G] > 0}
is minimal in the same sense.
Another significance of V(𝕎N) is that every member of 𝕎N is a convex combination (or weighted average) of vertices. So, a complete description of V(𝕎N) amounts to a complete description of 𝕎N, which in turn amounts to a very good description of either the entire collection of fair samples or the entire collection of correct samples.
Counting the Vertices of 𝕎N
Given a function w from Γ to [0,1], it is relatively easy to test whether w ∈ 𝕎N and whether w ∈ V(𝕎N) (see Theorem B.3 below), but counting all the vertices appears difficult, or at least slow, for large N.

A consequence of the theorem is that if w is a vertex of 𝕎N, then w(G) > 0 for at most N different sets G ∈ Γ. Call the collection {G ∈ Γ : w(G) > 0} the support of w, and denote it by Sup(w).
So, one way of enumerating the vertices of 𝕎N involves enumerating the bases of the vector space ℝN that have the form {IB1, IB2, …, IBN} where each Bi ∈ Γ, and solving a linear system for each such basis to find the unique values w1, w2, …, wN such that:

Then let w : Γ → ℝ be the function defined by:
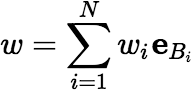
where for any sets G, H ∈ Γ,
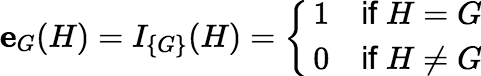
If each wi is nonnegative, then the function w so defined is a vertex of 𝕎N. Otherwise, w ∉ 𝕎N.
One complication here is the fact that the same vertex may be listed more than once, because the support of a vertex may not correspond to a complete basis for ℝN. (It is linearly independent, but it may have fewer than N members.) The algorithm can be adjusted to deal with this problem.
Obviously, enumerating the bases is a slow process when N is large, but any process of constructing all the vertices of 𝕎N will be slow because V(𝕎N) is so large. Counting the vertices when N is large would require additional mathematical insight into the problem (e.g., group actions and symmetries?).
An obvious upper bound for the size of V(𝕎N) is given by:
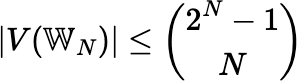
but this bound is not at all tight.
When G = {i1, i2, …, ik}, we may write eG as ei1, i2, …, ik . An example of a vertex in V(𝕎7) written using this notation is:
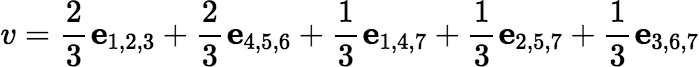
Its support is {{1,2,3}, {4,5,6}, {1,4,7}, {2,5,7}, {3,6,7}}. Its values are v({1,2,3}) = v({4,5,6}) = 2/3, v({1,4,7}) = v({2,5,7}) = v({3,6,7}) = 1/3, and v(G) = 0 if G is any other nonempty subset of L. (The column vectors I{1,2,3}, I{4,5,6}, I{1,4,7}, I{2,5,7}, and I{3,6,7} are linearly independent in ℝ7.)
The complete set of vertices of 𝕎3 is written below:

Another fairly simple and intuitive but less economical way of representing a function:

when N is small is to write the vectors IB1, IB2, …, IBk side by side as column vectors and to write the coordinates w1, w2, …, wk under the columns (omitting any columns for which wi = 0). The vertices of 𝕎3 are rewritten below using this notation:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1/2 | 1/2 | 1/2 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 1 | 1 |
| 0 | 1 |
| 1 | 0 |
| 0 | 1 |
| 1 | 1 |
| 0 | 1 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
| 1 |
| 1 |
| 1 |
| 1 |
Notice that all but one of these six vertices (v2) have supports that partition L. Vertices of this type are simple and easy to find—there is one for each partition of L—but they become relatively more rare as N increases. The number of such vertices is the N th Bell number BN. The first few Bell numbers (starting with N = 1) are: 1, 2, 5, 15, 52, 203, 877. [A000110] Compare these numbers to the vertex counts in Table 1.
Note that the last vertex, v6 or eL, is the function that maps L to 1 and every other member of Γ to 0. Call this vertex the trivial vertex. It corresponds to the trivial sample, which always includes every fragment in the lot. If S denotes the trivial sample, then Pr[S = G] = eL(G) × mG / mL, which equals 1 if G = L and 0 if G ≠ L.
Any vertex besides eL is called a nontrivial vertex. Any sample besides the trivial sample may be called a nontrivial sample. A proper sample is a sample S such that Pr[S = L] = 0. Obviously, a proper sample is nontrivial.
It can be shown that the trivial vertex eL
is connected to each other vertex of 𝕎N by an edge of the polytope.
So, if N > 1, then 𝕎N
can be considered a cone
with apex eL.
All the interesting structure of 𝕎N is found in the base of this cone.
The trivial vertex eL is the only member of 𝕎N whose 1-norm equals 1.
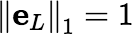
Every other point in the polytope has 1-norm greater than 1. The largest possible value for the 1-norm is N, and there is only one point in 𝕎N (a vertex) whose norm equals this maximum. It is the function w that maps each singleton subset of L to 1 and maps every other nonempty subset to 0. The sets {w ∈ 𝕎N : ‖w‖1 = r}, for 1 ≤ r ≤ N, partition 𝕎N into nonempty parallel slices.
There is a kind of duality relationship among points in the base of 𝕎N, which relates each point w ∈ 𝕎N to its dual w*. If w ∈ 𝕎N and w(L) = 0, then for ∅ ≠ G ⊂ L, define the dual of w by:
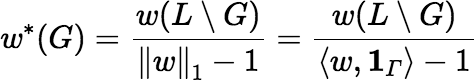
The dual operator defined here is different from, but in some ways similar to, the dual operator for a geometric algebra.
The support of w* consists of the complement of every set in Sup(w). If w(L) = 0, then w assigns a nonzero value to a subset ∅ ≠ G ⊂ L if and only if w* assigns a nonzero value to L \ G. It is easy to show that the dual operator is an involution, i.e., that w** = w. Also:
 and
and

If w is self-dual, i.e., if w* = w, then ‖w‖1 = 2. A vertex v ∈ V(𝕎N) is self-dual if and only if v is of the form I{G, L \ G} (a function in ℝΓ) for some ∅ ≠ G ⊂ L. The set of all self-dual w ∈ 𝕎N is a simplex of dimension 2N − 1 − 2, which is the convex hull of the collection of all self-dual vertices. For example, when N = 3, there are 3 self-dual vertices (v3, v4, and v5 above), and their convex hull is a 2-simplex.
The group of symmetries of 𝕎N includes all symmetries induced by permutations of the set L. The dual operator also permutes vertices of the polytope in a manner that preserves faces and adjacencies, although it does not preserve distances.
A simpler polytope (simpler than 𝕎N) is obtained if we add constraints to require that w(G) = w(H) whenever |G| = |H|. In this case the resulting polytope 𝕌N is a simplex of dimension N − 1, which has only N vertices, all of which are easily located. One can write the N vertices u1, u2, …, uN as follows:
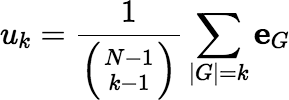 , for
k = 1, 2, …, N.
, for
k = 1, 2, …, N.The function uk is a vertex of 𝕎N if and only if k ∈ {1, N − 1, N}. So, not all the vertices of 𝕌N are vertices of 𝕎N unless N ≤ 3. In the case when N = 3, the three vertices u1, u2, and u3 are equal to v1, v2, and v6, respectively (see above).
For N > 2 the simplex 𝕌N is a small subset of 𝕎N. All the samples that can be obtained using the strategy described in Theorem B.1 are associated with functions w ∈ 𝕌N. So, if N > 2, there are many, many fair samples that cannot be obtained by the strategy of Theorem B.1.
It seems that either fair samples or correct samples derived from functions w
in 𝕌N are better than other fair or correct samples,
because they are more random. The type of sample that Gy uses to derive his
expression for the fundamental sampling variance
is essentially a correct sample of this type.
Group Actions
Perhaps the most obvious candidate to provide an interesting group action on 𝕎N is the symmetric group Sym(L) or SN, whose elements are all the permutations of the set L = {1, 2, …, N} and whose group operation is composition. If we compose permutations from left to right (in accordance with Keith’s training), the group acts on L on the right. There is an obvious way to make the same group act on the set Γ on the right. If G ∈ Γ and σ ∈ SN, then define:

It is only slightly less obvious how to make the group SN act on ℝΓ on the right. If w ∈ ℝΓ and σ ∈ SN, then define w • σ by:
 , for all
G ∈ Γ.
, for all
G ∈ Γ.This definition ensures that eG • σ = eG • σ . We also have the fact that the mapping w ↦ w • σ is a vector space automorphism. So, in particular, if w ∈ ℝΓ and we write:
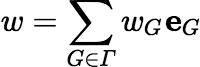
then:

When restricted to the polytope 𝕎N, this action becomes a right group action on 𝕎N. When restricted to the vertex set V(𝕎N), it becomes a right group action on V(𝕎N). In fact, if restricted to the p-faces of 𝕎N, for any 0 ≤ p ≤ 2N − N − 1, it becomes a group action on those p-faces.
The primary reason for considering group actions on V(𝕎N) is to count vertices of different types. The action of the group SN partitions V(𝕎N) into equivalence classes called orbits, the orbit of a vertex v being defined as:
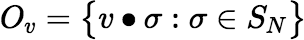
The size of the orbit Ov can be calculated from the size of the stabilizer of v, defined as:

which is a subgroup of SN. Since SN is finite,
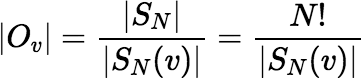
Finding and counting all the vertices in a given orbit Ov might be time-consuming, but it is conceivable that counting the permutations of L that leave v unchanged could be easier. Unfortunately there are complications, and it isn’t as easy as one might hope. Consider the six vertices of 𝕎3, which were listed above. Obviously any permutation of L leaves vertex v6 (eL) fixed, because it leaves L fixed. So, the stabilizer of v6 is the entire group SN. The only nontrivial permutation that leaves v3 fixed is the transposition (2,3), which leaves each member of Sup(v3) unchanged. So, the stabilizer of v3 is the cyclic subgroup of order 2 generated by (2,3). Similarly, the stabilizers for v4 and v5 are subgroups of order 2. Complications arise when we consider v1 and v2. Any nontrivial permutation of L moves at least two members of Sup(v1), but it does so in a way that preserves Sup(v1) itself (and the vertex) with no change. So, the stabilizer of v1 is the entire group SN (and similarly for v2).
In this example it is easy to recognize the orbits. There are four of them: {v1}, {v2}, {v3, v4, v5}, and {v6}.
Measure Theory
One can also analyze the problem of fair sampling using the language of measure theory. The functions
m :  (L) → [0, ∞)
and
A :
(L) → [0, ∞)
and
A :  (L) → [0, ∞)
can be viewed as finite positive measures on the measurable space
(L,
(L) → [0, ∞)
can be viewed as finite positive measures on the measurable space
(L,  (L)).
A function
w :
(L)).
A function
w :  (L) → [0, 1]
as described above leads to a positive measure
W :
(L) → [0, 1]
as described above leads to a positive measure
W : 
 (L) → [0, ∞)
on the measurable space
(
(L) → [0, ∞)
on the measurable space
( (L),
(L), 
 (L)).
A
(L)).
A sample space
is obtained from
( (L),
(L), 
 (L))
by providing it with a probability measure P.
Then the criterion for fair sampling is that:
(L))
by providing it with a probability measure P.
Then the criterion for fair sampling is that:
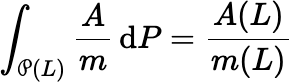
for any positive measure A defined on the measurable space
(L,  (L)). Rewriting,
(L)). Rewriting,

where the measure W is given by:
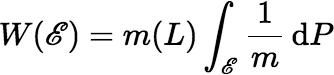
The measure W must satisfy the following condition:
 , for any positive measure A on
(L,
, for any positive measure A on
(L,  (L)).
(L)).In the case of a finite lot L with the discrete σ-algebra
 (L), the preceding requirement is equivalent to
requiring that:
(L), the preceding requirement is equivalent to
requiring that:
 , for any
j ∈ L,
, for any
j ∈ L,where δj denotes a Dirac measure.
The use of measure theory makes the problem look much simpler in some ways, and it suggests ways to analyze fair sampling of infinite lots, with more general σ-algebras.
Unbiased Splitting
Although for N ≥ 2 it is always possible to take a fair proper sample from the lot, it may not be possible to split the lot probabilistically into two or more fractions, each of which constitutes a fair sample. In general, it is possible to split the lot into two fractions in such a way that each fraction is a fair sample if and only if no fragment in the lot accounts for more than half the lot’s total mass. (A proof is available.) If N = 2, this generally is impossible, because the two fragments never have exactly the same mass, and one fragment always provides more than half the total mass. For typical lab samples with large N, fair splitting is usually possible.
Theorem B.4 shows how a 3-fragment lot can be split probabilistically into two fair samples.

The result in Theorem B.4 is derived by solving a system of linear equations.
Another easy way to split a 3-fragment lot fairly is to choose a random binary partition
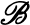 of the lot
with the probabilities given below and then choose one of the resulting subsets at random to be S.
of the lot
with the probabilities given below and then choose one of the resulting subsets at random to be S.
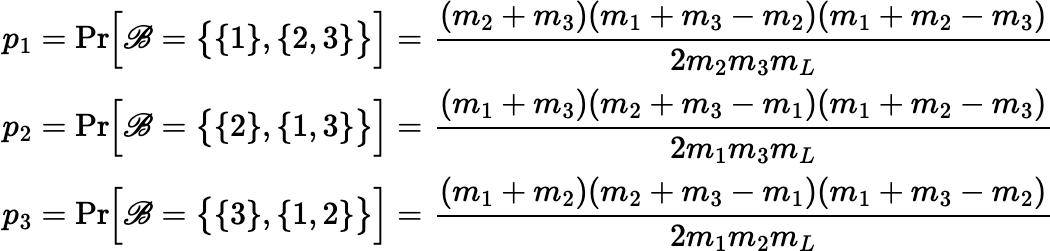
Then:
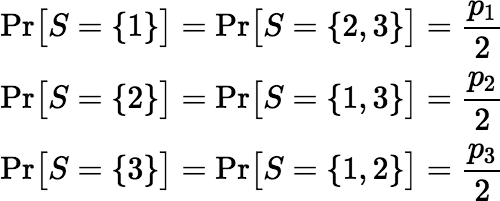
This scheme S is both fair and correct. In fact, the correctness of S does not depend
on how the random partition  is chosen. Given any random or fixed partition
is chosen. Given any random or fixed partition 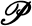 of L, of any size, a sample obtained by selecting one of the members of
of L, of any size, a sample obtained by selecting one of the members of
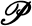 at random is always correct.
However, a careful choice of
at random is always correct.
However, a careful choice of 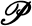 can guarantee that the
sample and its complement are also fair.
can guarantee that the
sample and its complement are also fair.
The same scheme can be extended to larger lots.
For N ≥ 3, choose a random binary partition 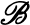 using the probabilities shown below:
using the probabilities shown below:
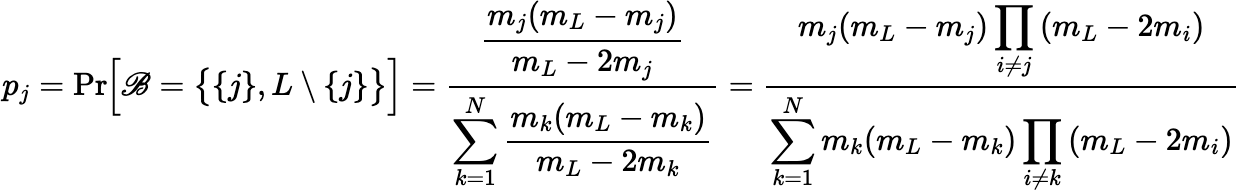
Then choose one of the two resulting fractions at random. The sample probabilities are given by:

The sample will always consist of either 1 or N − 1 fragments.
Notice that the final expression for pj works even when the mass of one fragment, mi, is exactly mL / 2, giving pi = 1 and pj = 0 for j ≠ i, whereas the expression before it fails because of division by 0 in that case.
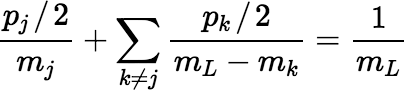
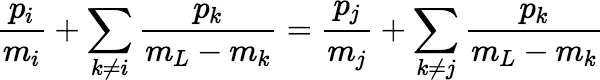

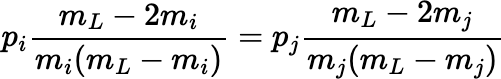
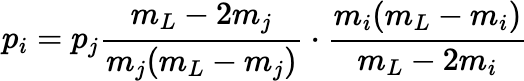

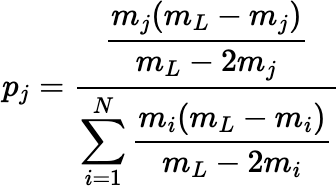
The preceding scheme can be generalized further.
If 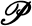 is a partition of L into three
or more fractions, P1, P2, …, Pk,
where each fraction Pi has mass less than mL / 2,
then a solution to the fair-splitting problem is given by:
is a partition of L into three
or more fractions, P1, P2, …, Pk,
where each fraction Pi has mass less than mL / 2,
then a solution to the fair-splitting problem is given by:
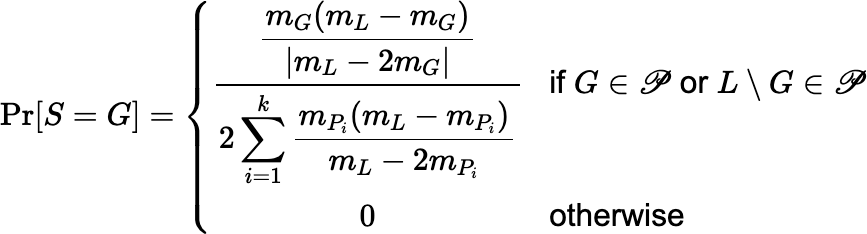
|
(∗) |
In all cases, Pr[S = G] = Pr[S = L \ G]. Both the sample S and the complementary sample L \ S are fair and correct. As before, this scheme can be extended to include the case where one fraction, Pi, weighs exactly mL / 2, in which case Pr[S = Pi] = Pr[S = L \ Pi] = 0.5.
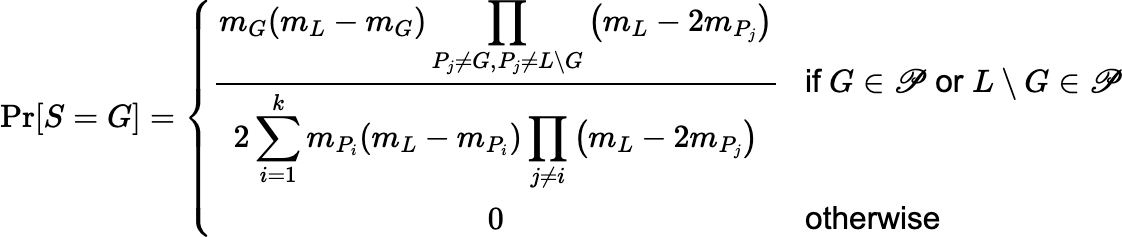
In general, if S is a fair sample such that Pr[S = G] = Pr[S = L \ G] for all G ⊆ L, then L \ S is also fair, because Pr[L \ S = G] = Pr[S = L \ G] = Pr[S = G] and S is fair. Furthermore, S and L \ S are both correct, since Pr[ j ∈ S] = Pr[ j ∈ L \ S] = 0.5.
Given m1, m2, …, mN, where each mj ≤ mL / 2, and a linear ordering of the proper, nonempty subsets G1, G2, …, G2N−2 ⊆ L, solving an underdetermined 2N × (2N − 2) linear system of rank 2N − 1 for the probabilities Pr[S = Gj], subject to nonnegativity constraints, will yield, at least in theory, all the solutions to the fair-splitting problem. The system can be represented as a matrix equation, Xp = J, where J denotes a column of 1’s, p is the column vector with entries pj = Pr[S = Gj], and X is the 2N × (2N − 2) matrix with entries given by:
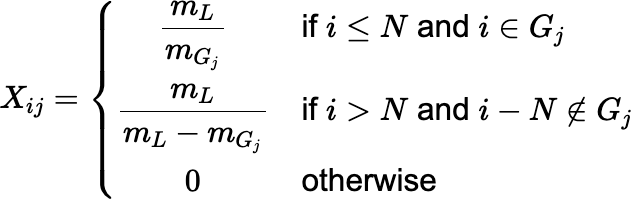
For N = 3, an explicit matrix equation is shown below.

The solution space in this case is one-dimensional. The size of the problem and the dimension of the solution space grow rapidly with N.
Note: Although this algebra can be done in terms of the functions w ∈ 𝕎N described above, there seems to be little advantage in doing so. The full set 𝕎N can be defined and investigated without reference to the fragment masses, whereas the subset consisting of those functions w that solve the fair-splitting problem cannot be.
All solutions of the linear system satisfy the requirement that the sum of the probabilities must equal 1. Solutions might fail to satisfy nonnegativity constraints; however, under the stated assumptions, the particular solutions given by (∗) above are always nonnegative, fair, and correct.
The unique, minimum-length algebraic solution to the equation is given by X +J, which can be obtained using a singular value decomposition of X, although the solution might fail to satisfy the nonnegativity constraints. This solution, if nonnegative, is also correct, with Pr[ j ∈ S] ≡ 0.5.
The entire solution space, whether constrained to be nonnegative or not, has a symmetry that allows transposing all the probabilities Pr[S = G] and Pr[S = L \ G] for one solution to obtain another. This operation is length-preserving; so, the minimum-length solution, X +J, remains fixed under it, as do the solutions given by (∗).
For N ≥ 3, the (2N − 2) × 1 column vector κ described below lies in the null space of X, implying that sufficiently small multiples of κ can be added to any particular solution to obtain new solutions, subject to the nonnegativity constraints.

The entire null space is the column space of the orthogonal projection matrix I − X +X, a basis for which can be found using a singular value decomposition of X.
For any p ≥ 2, if the mass of any fragment is more than mL / p, it is impossible to split the lot into p fractions such that each fraction Si is a fair sample (because if any Si is a fair sample, then Pr[ j ∈ Si] ≥ mj / mL for each fragment j). It seems likely that if each fragment weighs less than mL / p, then the lot can be split into p fair fractions, but no proof is offered here for p > 2.
As I said: For what it is worth….