Algorithms

Definitions

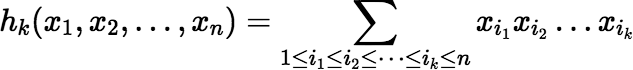
		(1)

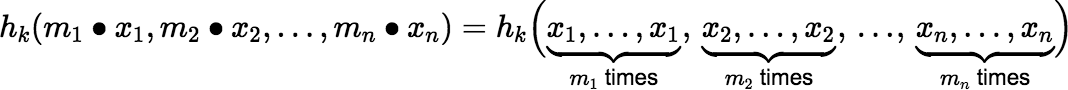
(2)

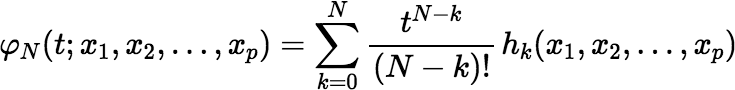
(3)

1. Incremental calculation of h_k(x₁, x₂, …, x_n), for increasing k, with O(n) increment step

1	for i = 1 to n loop
2		w_i ← 1		// w_i = h₀(x₁, x₂, …, x_i) = 1
3	end loop

4	for k = 1 to … loop
5		w₁ ← x₁ w₁		// w₁ = h_k(x₁) = x₁^k
6		for i = 2 to n loop
7			w_i ← w_i − 1 + x_i w_i	// w_i = h_k(x₁, x₂, …, x_i)
8		end loop
9		output w_n		// w_n = h_k(x₁, x₂, …, x_n)
10	end loop

2. Incremental calculation of h_k(m₁ • x₁, m₂ • x₂, …, m_n • x_n) — which may be useful when ∑ m_i ≫ n

1	y ← 1			// `y = h₀(m₁ • x₁, …, m_n • x_n)`

2	for i = 1 to n loop
3		w_i ← 0
4	end loop

5	for k = 1 to … loop
6		s ← 0
7		for i = 1 to n loop		// O(n) loop
8			w_i ← x_i (w_i + m_i y)
9			s ← s + w_i
10		end loop
11		y ← s / k		// y = h_k(m₁ • x₁, …, m_n • x_n)
12		output y
13	end loop

The same algorithm may be useful when the m_i are not integers (e.g., when calculating a convolution of gamma distributions with varying scale parameters). In this case the algorithm outputs for each k the value:

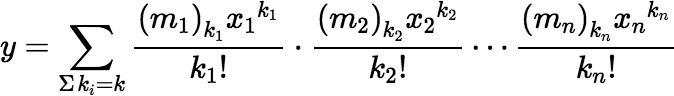
3. Incremental calculation of φ_k(t; x₁, x₂, …, x_n)

1	for i = 0 to n loop
2		w_i ← 1		// w_i = φ₀(t; x₁, x₂, …, x_i) = 1
3	end loop

4	for k = 1 to … loop
5		w₀ ← w₀ t / k		// w₀ = φ_k(t; ~) = t^k / k!
6		for i = 1 to n loop		// O(n) loop
7			w_i ← w_i − 1 + x_i w_i	// w_i = φ_k(t; x₁, x₂, …, x_i)
8		end loop
9		output w_n		// w_n = φ_k(t; x₁, x₂, …, x_n)
10	end loop

4. If G(s) is the rational function:

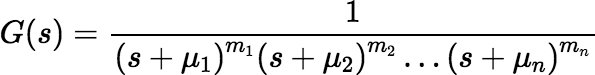
then the inverse Laplace transform of G(s) is the function:

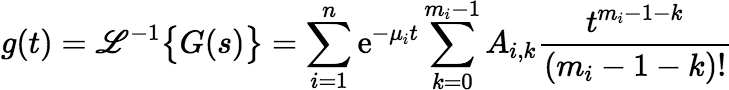
where A_i, k is given by:

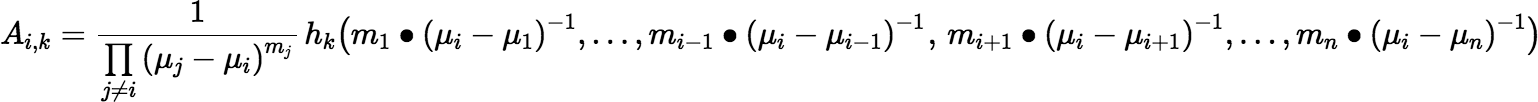
If one modifies G(s) by incrementing m_j for some 1 ≤ j ≤ n, then g(t) is replaced by (g ∗ D_{μ_j})(t), and the coefficients A_i, k change as shown below:

1	s ← 0

2	for i = 1 to n loop
3		if i ≠ j then
4			A_i, 0 ← A_i, 0 / (μ_j − μ_i)
5			for k = 1 to m_i − 1 loop
6				A_i, k ← (A_i, k − A_{i, k − 1}) / (μ_j − μ_i)
7			end loop
8			s ← s + A_{i, m_i − 1}
9		end if
10	end loop

11	A_{j, m_j} ← −s				// new coefficient
12	m_j ← m_j + 1

If j = n + 1 so that we are including a new factor (s + μ_n + 1) in the denominator of G(s), insert the line m_j ← 0 before line 1 and append the line n ← n + 1 after line 12.

If the value of g(t) is needed only for a specific value of t, and if it is known that one m_j will be incremented repeatedly and no other m_i will increase, then a different version of the algorithm can be used to recalculate A_i, k only for i ≠ j, without accumulating the sum s. The sum of all the A_j, k terms can be recalculated at each iteration using the φ function above without calculating the individual coefficients A_j, k.

Note: Given any function g(t) of the form:

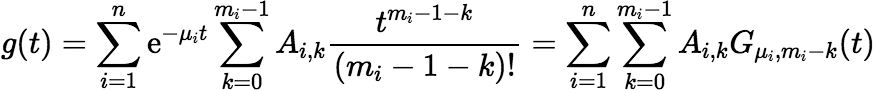
with arbitrary coefficients A_i, k, if we wish to calculate (g ∗ D_{μ_j})(t), the same algorithm for updating the coefficients works. However, the shortcut method of evaluating g(t) using the φ function is not guaranteed to work for arbitrary A_i, k.